4 Nisan 2014 Cuma
Kesirlerin Mezopotamyalılarda tarihçesi
MEZOPOTAMYALILARDA KESİR SAYILARI
Mezopotamya'da rakamların göstereceği sayıları, yani değerleri kesin olarak
belirlemek mümkün değildi. Örneğin, 1, 60 ve 1/60 formülü ile ifade edilebilecek
çeşitli değerleri aynı sembol temsil ediyordu. Bu sebolün hangi değeri ifade ettiğini
belirlemek bu rakam sisteminde mümkün değildi, ancak metin ve konu yardımıyla
belirlenebiliyordu.
Mezopotamya rakamlarının konumsal ve altmış tabanlı olma özelliği sadece tam
sayılar için değil, kesirler içinde geçerliydi. işareti 1x60=1, 1x60= 3600,
sayılarını gösterebileceği gibi, 1x 60=1, 1x60=1/3600 gibi kesirleri de
gösterebiliyordu.
Kesirlerin Mısırlılarda Tarihçesi
MISIRLILARDA KESİR SAYILARI VE KULLANILIŞI
Kesirli sayıları özel işaretlerle anlatıyorlardı. Bu işaretleri kuş şeklindeki tanrıları olan
Horus’un gözünü temsil eden şekillerden bulmuşlardı. İnanışlarına göre Horus’un
gözünü Seth adlı parçalamıştı. Toth adlı tanrı bu parçaları birleştirip Horus’u yeniden
göz sahibi yapmıştı. Bu parçaların toplamı 63/64 idi. Bu sebeple Toth’un sihir ile
noksanı tamamladığına inanıyorlardı.
Mısırlılarda kesir işareti şeklinde idi. Bu işaret kesrin payını 1 olarak ifade
ediyor ve paydayı temsil eden rakamın üst kısmına koyuyordu. Böylece
işareti 1/3’ü temsil etmektedir. Bu şekildeki sınırlı kesir sembollerinin de istisnaları
vardı. Örneğin 1/2, 1/4, 1/8, 1/16, 1/32 ve 1/64 için başka özel işaretler de
kullanılıyordu. Bunlar Mısırlıların doğan kuşu şeklindeki tanrıları olan Horus’un
gözünü temsil etmekteydi
Geleneğe gore, Horus’un gözü Seth adlı tanrı tarafından parçalanmıştı. Bu parçaları
Thot adlı tanrı (ibis kuşu ile temsil edilen tanrı) bir araya getirerek Horus’u yeniden
göz sahibi etmişti. Bu gözün muhtelif kısımlarını temsil eden kesirlerin toplamı 63/64
etmektedir. Bu sebeple, Thot’un sihir yoluyla buradaki noksanı tamamladığı Kabul
edilmekteydi.
Mısır rakamlarının oldukça ilkel bir vasıf taşımalarına rağmen bunlar tarihte bilinen ilk
ve en eski rakamlar arasında bulunmakla büyük bir değer ve önem taşırlar. Çünkü
bunlar sayıların belirli sembollerle ifade edilmesi zihniyet ve düşüncesinin ilk
örneklerinden, belki sadece Sümerliler istisna edilirse, en eskisini temsil etmektedirler
Eski Mısırlıların kesir anlayışının ana karekteristiği payların daima 1 oluşu, örneğin
62/64 gibi bir kesrin kullanılmamış olmasıdır. Payları 1 olmayan kesirleri payları 1
olan kesirlerin toplamı şeklinde ifade ederlerdi.
Bununla birlikte sayıları çok az olmakla birlikte, 1 paylı kesirlere istisnalar vardı.
Bunlar arasında sadece 2/3 kesri sık sık, 3/4, 4/5 ve 5/6 kesirleri de nadiren
kullanılıyordu. Bu kesirle matemetikte kullanılmakta ve her biri özel bir işaretle temsil
edilmekte idi. Horus’un gözünün kısımları ile ifade edilen işaretler ise matematik
işlemlerinden fazla hububat ölçülerinde kullanılıyordu.
Hiç şüphesiz, Mısırlılar kesirlere ayrı bir sayı grubu olarak bakma safhasına
erişmemiş bulunuyorlardı ve zihinlerinde kesir kavramı henüz genelleştirilmemişti.
Mısır aritmetiğinde bir kesrin payı 1 ‘den farklı olunca, böyle bir kesre
tamamlanmamış bir bölme işlemi, çözülmemiş bir problem gözüyle bakılmış olduğu
söylenebilir. Çünkü böyle bir kesri payları 1 olan kesirler toplamı şekline sokmak
ihtiyacını duyuyorlardı. Demek ki böyle kesirleri gerçek kesir kabul etmiyorlardı. Böyle
olunca da, Mısır aritmetiğinde genel bir kesir kavramının mevcut olmadığı sonucuna
kolayca varılabilir.
Payların hep 1 olmasında gösterilen bu ısrar belki de kesirlerin biriminden küçük
nicelikler şeklinde tasavvur edilmiş olduğunu göstermekte olabilir. Başka bir deyimle,
bu kesirler olasılıkla birimin örneğin ikiye, üçe, dörde, beşe, altıya bölünmesini ifade6
ediyordu. Fakat her nedense bu birim paylı kesirlerin katsayılarını almıyorlar, daha
doğrusu, bunları kesir saymıyorlardı. Buna belki de bu gibi kesirleri ifade etmek için
kelimelerinin noksan oluşu veya sembollerinin bulunmayışı, ayrı ayrı ya da birlikte,
sebep olmuş olabilir. Yukarıda sözü geçen istisnaların, yani 2/3, 3/4, 4/5 ve 5/6
kesirlerinin hepsinin de 1/3, 1/4, 1/5 ve 1/6 gibi birim paylı kesirleri birime
tamamlamakta olmaları da ilgi çekicidir.
Mısırlıların dilinde özel adı bulunan kesirler 2/3, 1/3, 1/2, 1/4 ve belki de 1/6 ve 1/8
kesirleriydi. 2/3’ün adı “iki kısım”, 1/3’e “üçünçü kısım”dı. Yunancada da, 2/3’e “iki
kısım”, 1/3’e “üçüncü kısım”, 3/4’e “üç kısım”, 1/4’e “dördüncü kısım” deniyordu.
Türkçede, yarım ve çeyrek, Arapçada nısıf, sülüs, rubu....gibi kelimelerde olduğu gibi
özel adları olan kesirlere “tabii kesirler” adı verilebilir. Arapçada 2/3, 2/4, 2/5 ve genel
olarak 2/n gibi kesirlerin de bu anlamda “tabii kesirler” sayılması akla gelebilir.
Mısır matematikçiler, kesirlerin zikri geçen ana özelliği dolayısıyla, mesela 17’yi 5’e
bölünce bulunacak “3 tam 2/5 sonucunun kesir kısmını payları birim olan kesirler
toplamında, yani 1/15 + 1/3 ile, sonucu da 3 + 1/3 + 1/15 şeklinde ifade ediyorlardı.
Aynı suretle, örneğin 7 somun ekmeği 9 ya da 10 kişi arasında eşit bölmek icap etse,
7/9 ve 7/10 bölümlerini, payları 1 olan kesirler şeklinde ifade ediyorlardı. Böylece
7/9=1/3 +1/3 + 1/9 = 2/3 + 1/9 ve 7/10 = 1/2 +1/5 sonuçları elde edilmekteydi. Bunlar
arasında 2 X 1/41=1/24 +1/246 +1/328 ve 2 X 1/43 = 1/42 +1/86 + 1/129 + 1/301 gibi
oldukça kafa karıştırıcı eşitlikler yer almaktadır.
Kesirlerle işlemlere gelince, payları 1 olduğuna göre, kesirlerin toplamını bulma işlemi
Mısır matematikçileri için, tabiatıyla bir mesele teşkil etmemekte idi. Çünkü Mısırlı
matematikçi, toplama yapmak için böyle kesirleri peş peşe yazmakla yetiniyordu.
Örneğin, 1/3, 1/5 ve 1/2’nin toplamı 1/2 + 1/3 +1/5’tir. Toplama işlemi bundan ibaretti.
Yalnız, sonuç da 1/n şeklinde ifade edilebilince, toplam bir tek kesirle ifade
edilmekteydi.
Kesirler
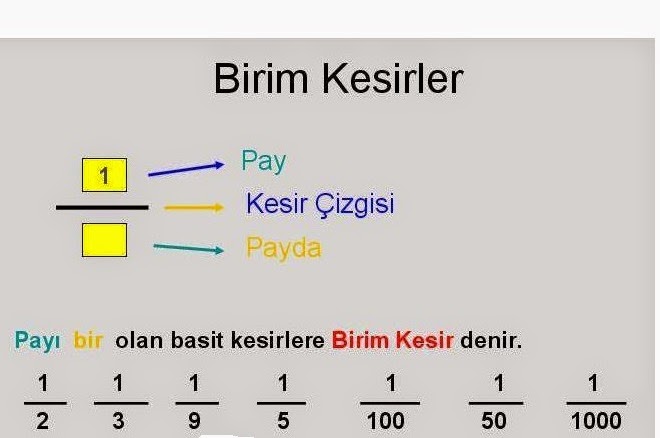
Kesir: Bir bütünün eş parçalarını gösteren, a/b şeklinde yazılabilen ifadelere kesir denir. Kesirleri gösterirken ortaya kesir çizgisi çizilir, çizginin üstünde pay, altında payda olur. Payda bir bütünün kaç eşit parçaya ayrıldığını, pay ise bu parçalardan kaçının alındığını veya tarandığını gösterir.
 |
Not: Bir sayının sıfıra bölümü tanımsızdır. Bir bütünü sıfır parçaya ayıramayacağımız için paydada sıfır bulunamaz.
Kesirlerde Karşılaştırma ve Kesirlerin Sıralanması
Kesirleri önceki konumuzda anlatmıştık, şimdi ise kesirleri karşılaştırma ve sıralamayı öğrenelim.
KESİRLERDE KARŞILAŞTIRMA VE KESİRLERİN SIRALANMASI
Kesirlerde sıralama işlemi yaparken kesirleri birbirleri ile karşılaştırırız. Karşılaştırma ve sıralama işlemini küçüktür ( < ), büyüktür ( > ) ve eşittir ( = ) sembolleriyle yaparız. Payları eşit olan kesirlerde sıralama, paydaları eşit olan kesirleri sıralama, tam sayılı kesirlerde sıralama, bir doğal sayı ile kesrin karşılaştırılması, yarıma yakınlığa bakarak karşılaştırma ve bütüne yakınlığa bakarak karşılaştırmayı görelim.
1) PAYLARI EŞİT OLAN KESİRLERİ SIRALAMA: Payları eşit olan kesirleri sıralamak için kesirlerin paydalarına bakarız. Paydası küçük olan kesir daha büyüktür. Örneği inceleyelim:
2) PAYDALARI EŞİT OLAN KESİRLERİ SIRALAMA: Paydaları eşit olan kesirleri karşılaştırmak için paylarına bakarız. Payı büyük olan kesir daha büyüktür. Örnek:
3) PAYLARI VE PAYDALARI EŞİT OLMAYAN KESİRLERİ SIRALAMA
Pay ve paydaları eşit olmayan kesirleri karşılaştırabilmek için öncelikle kesirlerin paylarını veya paydalarını eşitleriz. Paylarını veya paydalarını eşitlemekten hangisi kolay oluyorsa onu yapabiliriz. Eşitledikten sonra yukarıda gördüğümüz şekilde karşılaştırır ve sıralarız.
4) TAM SAYILI KESİRLERİ SIRALAMA
Tam sayılı kesirleri karşılaştırırken iki yol izleyebiliriz. Önce tam sayılı kesri bileşik kesre çevirme işlemi yaparız, daha sonra yukarıda öğrendiğimiz gibi paylarını veya paydalarını eşitleyerek karşılaştırırız. Tam sayılı kesirlerde tam kısmı büyük olan kesir daha büyüktür. Eğer tam kısımları eşitse kesir kısımlarını karşılaştırırız. Kesir kısımlarını karşılaştırmayı da yukarıda öğrenmiştik.
5) BÜTÜNE YAKINLIK
Kesirlerin tam sayılara yakınlıklarına göre karşılaştırma yapabiliriz.
Örnek: 4/5 ve 7/8 kesirlerini karşılaştıralım. 4/5 birden küçüktür ve bütüne (1'e) olan uzaklığı 1/5'tir. 7/8 birden küçüktür ve bütüne (1'e) olan uzaklığı 1/8'dir. 1/8 kesri 1/5'ten daha küçük bir kesir olduğu için 7/8 kesrinin 1 tama olan mesafesi daha azdır. Yani daha yakındır. Buradan 7/8 > 4/5 sıralamasını yapabiliriz.
Örnek: 11/5 ve 17/8 kesirlerini karşılaştıralım. 11/5 kesri 2 tamdan büyüktür ve 2 tamı 1/5 geçmiştir. 17/8 kesri 2 tamdan büyüktür ve 2 tamı 1/8 geçmiştir. 1/8 kesri 1/5'ten daha küçük bir kesir olduğu için 17/8 kesri daha küçüktür. Çünkü iki kesir de 2 tamı geçmiştir. Ancak 17/8 kesri tamı 1/8 geçmiştir, diğeri 1/5 geçmiştir. 1/8 daha küçük olduğu için 17/8 daha az geçmiştir. Buradan 17/8 < 11/5 sıralamasını yapabiliriz.
6) YARIMA YAKINLIK
Kesirlerin yarıma (1/2'ye) yakınlıklarına göre karşılaştırma yapabiliriz.
Örnek: 9/20 ve 11/24 kesirlerini karşılaştıralım. 9/20 kesri yarımdan (10/20) küçüktür ve yarıma olan uzak 1/20'dir. 11/24 kesri yarımdan (12/24) küçüktür ve yarıma olan uzak 1/24'tür. 1/24 kesri 1/20'den daha küçük bir kesir olduğu için 11/24 kesrinin yarıma olan mesafesi daha azdır. Yani daha yakındır. Buradan 11/24 > 9/20 sıralamasını yapabiliriz.
Örnek: 11/20 ve 17/32 kesirlerini karşılaştıralım. 11/20 kesri yarımdan (10/20) büyüktür ve yarımı 1/20 geçmiştir. 17/32 kesri yarımdan (16/32) büyüktür ve yarımı 1/32 geçmiştir. 1/32 kesri 1/20'den daha küçük bir kesir olduğu için 17/32 kesri daha küçüktür. Çünkü iki kesir de yarımı geçmiştir. Ancak 17/32 kesri yarımı 1/32 geçmiştir, diğeri 1/20 geçmiştir. 1/32 daha küçük olduğu için 17/32 daha az geçmiştir. Buradan 17/32 < 11/20 sıralamasını yapabiliriz.
KESİRLERDE KARŞILAŞTIRMA VE KESİRLERİN SIRALANMASI
Kesirlerde sıralama işlemi yaparken kesirleri birbirleri ile karşılaştırırız. Karşılaştırma ve sıralama işlemini küçüktür ( < ), büyüktür ( > ) ve eşittir ( = ) sembolleriyle yaparız. Payları eşit olan kesirlerde sıralama, paydaları eşit olan kesirleri sıralama, tam sayılı kesirlerde sıralama, bir doğal sayı ile kesrin karşılaştırılması, yarıma yakınlığa bakarak karşılaştırma ve bütüne yakınlığa bakarak karşılaştırmayı görelim.
1) PAYLARI EŞİT OLAN KESİRLERİ SIRALAMA: Payları eşit olan kesirleri sıralamak için kesirlerin paydalarına bakarız. Paydası küçük olan kesir daha büyüktür. Örneği inceleyelim:
2) PAYDALARI EŞİT OLAN KESİRLERİ SIRALAMA: Paydaları eşit olan kesirleri karşılaştırmak için paylarına bakarız. Payı büyük olan kesir daha büyüktür. Örnek:
3) PAYLARI VE PAYDALARI EŞİT OLMAYAN KESİRLERİ SIRALAMA
Pay ve paydaları eşit olmayan kesirleri karşılaştırabilmek için öncelikle kesirlerin paylarını veya paydalarını eşitleriz. Paylarını veya paydalarını eşitlemekten hangisi kolay oluyorsa onu yapabiliriz. Eşitledikten sonra yukarıda gördüğümüz şekilde karşılaştırır ve sıralarız.
4) TAM SAYILI KESİRLERİ SIRALAMA
Tam sayılı kesirleri karşılaştırırken iki yol izleyebiliriz. Önce tam sayılı kesri bileşik kesre çevirme işlemi yaparız, daha sonra yukarıda öğrendiğimiz gibi paylarını veya paydalarını eşitleyerek karşılaştırırız. Tam sayılı kesirlerde tam kısmı büyük olan kesir daha büyüktür. Eğer tam kısımları eşitse kesir kısımlarını karşılaştırırız. Kesir kısımlarını karşılaştırmayı da yukarıda öğrenmiştik.
5) BÜTÜNE YAKINLIK
Kesirlerin tam sayılara yakınlıklarına göre karşılaştırma yapabiliriz.
Örnek: 4/5 ve 7/8 kesirlerini karşılaştıralım. 4/5 birden küçüktür ve bütüne (1'e) olan uzaklığı 1/5'tir. 7/8 birden küçüktür ve bütüne (1'e) olan uzaklığı 1/8'dir. 1/8 kesri 1/5'ten daha küçük bir kesir olduğu için 7/8 kesrinin 1 tama olan mesafesi daha azdır. Yani daha yakındır. Buradan 7/8 > 4/5 sıralamasını yapabiliriz.
Örnek: 11/5 ve 17/8 kesirlerini karşılaştıralım. 11/5 kesri 2 tamdan büyüktür ve 2 tamı 1/5 geçmiştir. 17/8 kesri 2 tamdan büyüktür ve 2 tamı 1/8 geçmiştir. 1/8 kesri 1/5'ten daha küçük bir kesir olduğu için 17/8 kesri daha küçüktür. Çünkü iki kesir de 2 tamı geçmiştir. Ancak 17/8 kesri tamı 1/8 geçmiştir, diğeri 1/5 geçmiştir. 1/8 daha küçük olduğu için 17/8 daha az geçmiştir. Buradan 17/8 < 11/5 sıralamasını yapabiliriz.
6) YARIMA YAKINLIK
Kesirlerin yarıma (1/2'ye) yakınlıklarına göre karşılaştırma yapabiliriz.
Örnek: 9/20 ve 11/24 kesirlerini karşılaştıralım. 9/20 kesri yarımdan (10/20) küçüktür ve yarıma olan uzak 1/20'dir. 11/24 kesri yarımdan (12/24) küçüktür ve yarıma olan uzak 1/24'tür. 1/24 kesri 1/20'den daha küçük bir kesir olduğu için 11/24 kesrinin yarıma olan mesafesi daha azdır. Yani daha yakındır. Buradan 11/24 > 9/20 sıralamasını yapabiliriz.
Örnek: 11/20 ve 17/32 kesirlerini karşılaştıralım. 11/20 kesri yarımdan (10/20) büyüktür ve yarımı 1/20 geçmiştir. 17/32 kesri yarımdan (16/32) büyüktür ve yarımı 1/32 geçmiştir. 1/32 kesri 1/20'den daha küçük bir kesir olduğu için 17/32 kesri daha küçüktür. Çünkü iki kesir de yarımı geçmiştir. Ancak 17/32 kesri yarımı 1/32 geçmiştir, diğeri 1/20 geçmiştir. 1/32 daha küçük olduğu için 17/32 daha az geçmiştir. Buradan 17/32 < 11/20 sıralamasını yapabiliriz.
Kesirlerde Genişletme ve Sadeleştirme
Kesirleri önceki konumuzda anlatmıştık, şimdi ise kesirleri genişletmeyi ve sadeleştirmeyi öğrenelim.
KESİRLERİ GENİŞLETME
Bir kesrin pay ve paydasını aynı sayı ile çarparsak kesrin değeri değişmez. Buna kesirlerin genişletilmesi denir. Örnek olarak inceleyelim:
KESİRLERİ SADELEŞTİRME
Bir kesrin pay ve paydasını aynı sayıya bölersek kesrin değeri değişmez. Buna kesirlerin sadeleştirilmesi denir. Örneği inceleyelim:
KESİRLERİ GENİŞLETME
Bir kesrin pay ve paydasını aynı sayı ile çarparsak kesrin değeri değişmez. Buna kesirlerin genişletilmesi denir. Örnek olarak inceleyelim:
KESİRLERİ SADELEŞTİRME
Bir kesrin pay ve paydasını aynı sayıya bölersek kesrin değeri değişmez. Buna kesirlerin sadeleştirilmesi denir. Örneği inceleyelim:
Kesir Çeşitleri
KESİR ÇEŞİTLERİ
1) BASİT KESİRLER Payı: Paydasından küçük olan kesirlere basit kesir denir.

Birim Kesir: Payı 1 olan basit kesirlere birim kesir denir.
2) BİLEŞİK KESİRLER: Payı paydasına eşit veya payı paydasından büyük olan kesirlere bileşik kesir denir.
3) TAM SAYILI KESİRLER: Bir tam sayı ve bir basit kesir ile ifade edilen kesirlere tam sayılı kesir denir.
TAM SAYILI KESRİ BİLEŞİK KESRE ÇEVİRME
Bir tam sayılı kesiri bileşik kesre dönüştürürken kesrin paydası ile tam sayı çarpılır ve bulunan sonuca kesrin payı eklenerek paya yazılır.
BİLEŞİK KESRİ TAM SAYILI KESRE ÇEVİRME
Bir bileşik kesri tam sayılı kesre dönüştürürken kesrin payı paydasına bölünür, bu bölme işlemindeki bölüm tam kısma, kalan paya yazılır, payda ise değiştirilmeden aynen yazılır.
Kaydol:
Yorumlar (Atom)